Throw accuracy is a controversial and poorly understood rating in Madden 13. Many quarterbacks who have high throw accuracy ratings frustrate players who have difficulty hitting open wide receivers with them (cough, cough Matt Ryan). One reason for this is Madden 13 divides accuracy into short, medium, and deep accuracy. The throw accuracy rating is not a single rating but a combination of these three ratings.
Warning: Math Ahead!
We ran a multiple regression analysis to determine the relative contributions of short accuracy, medium accuracy and deep accuracy to the throw accuracy rating. Our data set was the publicly released EA Sports complete player roster for Madden 13. We assumed that the short, medium, and deep accuracy ratings were independent.
Our regression analysis indicated that all three sub-ratings significantly contributed to the throw accuracy rating. The equation that best predicted the throw accuracy rating was THA = -1.7 + 0.641*SAC + 0.308*MAC + .060*DAC. This accounted for approximately 90% of the variability in the throw accuracy rating. This means that a quarterback with 0 in all three sub-ratings would have a predicted throw accuracy rating of -1.7. Even though this is obviously not possible, the quarterback accuracy sub-ratings were high enough for us to disregard this. For every one point increase in short accuracy rating, the throw accuracy rating would increase by 0.641 points. Similarly, for every 1 point increase in deep accuracy rating, the throw accuracy rating would increase by 0.060 points. This means that in general, short accuracy rating contributes about ten times as much to the throw accuracy rating as the deep accuracy rating does.
These weights do not accurately reflect the preferences of madden players. Therefore the throw accuracy rating as judged by the game is not representative of throw accuracy in a typical player vs player game. To illustrate the effect of different weights on throw accuracy, we adjusted the equation for throw accuracy such that the relative weights of short accuracy and deep accuracy were flipped (ADJUSTED THA = -1.7 + .0.060*SAC + 0.308*MAC + 0.641*DAC). We then compared the throw accuracy rating to our adjusted rating.
Okay The Math is Over!
For those of you who skipped or did not understand the math section, we developed an adjusted throw accuracy rating that we believe better represents the actual throw accuracy of quarterbacks in player vs. player games.
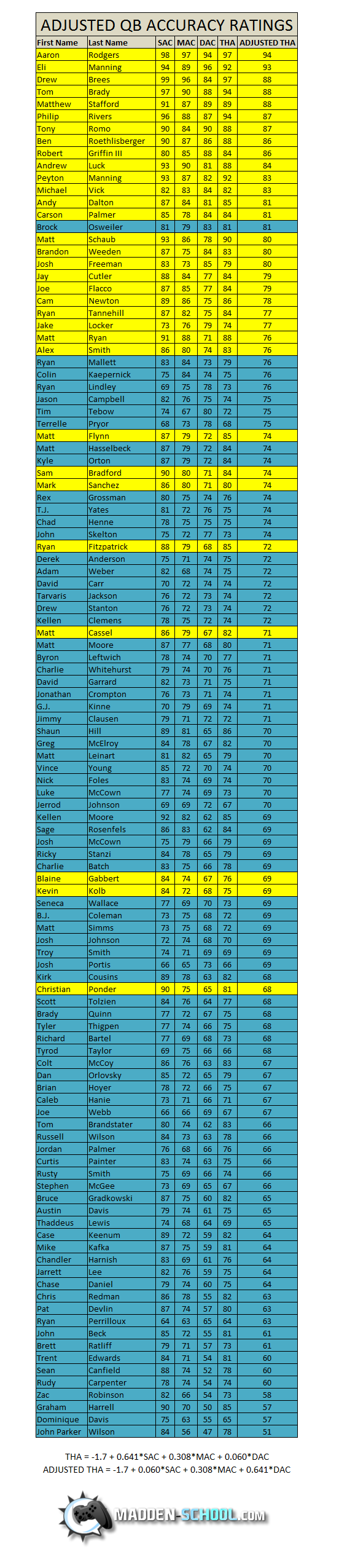
Below is a table comparing the game derived throw accuracy to our adjusted value. The quarterbacks are ranked by adjusted throw accuracy. Starters (or presumed starters) are highlighted in yellow. Backup quarterbacks are highlighted in teal.
Embed This Analysis on Your Site: Copy and Paste the Code Below
We found some results that did not surprise us based on player complaints. For instance, Matt Ryan is tied for the 24th best adjusted accuracy with such superstar quarterbacks as Ryan Mallett, Colin Kapernick, and Ryan Lindley. Another quarterback that often frustrates players, Matt Schaub, has his accuracy decrease from a game value of 90 to an adjusted value of 80, making him similiar to Josh Freeman and Brandon Weeden.
However, this also produced several surprises. First, both Robert Griffin III and Andrew Luck have higher adjusted accuracy ratings than 3 time NFL MVP Peyton Manning. Second, the notoriously inaccurate Tim Tebow has an adjusted accuracy of 75 while Mark Sanchez, who has a game accuracy rating 8 points higher, has an adjusted accuracy of only 74. Third, Brock Osweiler has an adjusted accuracy rating in the top 15, which is by far the best of any backup and is in fact better than 18 starters.
What does this mean for your madden experience? We have a few suggestions. Aaron Rodgers and Eli Manning grade out at least 5 points higher than any other quarterback including Drew Brees (game THA = 97). We also suggest that starting Tim Tebow is a viable strategy for Madden players who use the Jets, especially considering his advantages over Mark Sanchez in speed and throw power. Connected careers players may want to seriously consider any reasonable offer made for Peyton Manning as his backup (Brock Osweiler) is only 2 points worse in adjusted throw accuracy rating and has higher throw power. Also, Robert Griffin III and Andrew Luck appear to be especially valuable in connected careers given that they are already top 10 quarterbacks by our adjusted throw accuracy measure.
Our methods can also be applied to individual playing styles. We suggest that your actual throw accuracy rating is a weighted average of the short, medium, and deep accuracy ratings with the weights proportional to the number of short, medium, and deep pass plays you typically run (go back and read the math section if you want to know what we mean). This suggests that you may be frustrated with a quarterback because he does not fit your playing style.
Madden School Pro Tip: Find a quarterback whose short, medium and deep accuracy ratings best fit your playing style. The game accuracy ratings do not take into account how you use your quarterback.


Very nice and well done
Can you run a regression analysis or simulation to determine the average expected gain for every single play with each team against 4-3 cover 2
There would be 2 giant sources of error with that. The first would be human error and the second would be the randomness that is built into the game. At this point we haven’t found a good way to control for these things.
It would be nice to have a bunch of madden users joining together for a project of cataloging plays so combined we can get a huge sample size. Like have a google spreadsheet. Each player is responsible for 3 or 4 plays out of a particular formation and they map all the details they can including error, mis-clicks (square WR instead of circle) and misreads which could then be devalued as weighting towards the total calculated expectation. Together we can all determine what has highest success rate and average yards gained per play and try to account for situations as well.
Based upon the completion percentage on a given play and distribution of yards per play you can determine an exact “expected” point value of a particular play. A bit complicated, but say you can get an average expected 4 yard run. This number based on the exact probability distribution will leave you with 3rd and short x% of the time. Based on a conversion percentage on 3rd and short for that play of say 60% and the probability of getting in that situation, you can estimate the probability of getting a first down. Based upon that, you can then calculate the probability of getting 8 consecutive first downs, and if you have say 75% chance, that means each drive from the 20 yard line using that method has an expectation of about 75% of a TD.There’s more that goes into this but the site advancedNFLstats.com has gone into details about how they were able to come up with a chart based on NFL games on when you should go for it from what down and distance. That is based upon history of data,and due to variable change it might be different in a different situation…. For example, a team that converts a higher percentage of the time against a defense that gives up conversions a higher percentage of the time, it would be correct to go for it much more often, and much less often if the matchup is tough. Nevertheless, in Madden, I imagine the conversions on offense are a bit higher, but turnovers are as well, and that value your opponent has in the event of a turnover at any point of the field is probably higher than real NFL. This could be calculated with enough data, but would differe depending upon the specific play. Ultimately though, based upon the success rate in short yardage situations as well as long using certain plays from certain down and distance, one could calculate a game theory based approach to optomize the expected probability of a win. Game to game it would differ based upon specific opponents so minor adjustments to deviate from that baseline could be made, but I think it’s a project that could drastically change not only how gaming s played, but also many of the findings could translate into the NFL. Of course there is a high degree of variability and a ton of counter moves, but if opponent knows what play you are going to run, there are still probable some plays that can accomplish a lot. I think there are a lot of approaches to the game of poker which actually can apply to football. David skalanski started with assumption if opponent could see your cards, what would be the ideal move. Well in Madden, if opponent knows you run the same play every time, what play works best on 1st and 10? and all other down and distances? Obviously it depends on team strength and playbook, but if we work on one playbook a week and one team a week we could get through 32 teams. Once you accomplish that there were many that advanced game theory in poker farther. Given opponents only know a range of cards (plays) you might call, now which plays are best knowing opponent can’t just guess?
Anyways all of this is too much work for any individual to undertake on his own, but I for example specialize in the Vikings playbook, If I knew there were going to be 31 other players putting in the work to catelog there playbooks, I would have no problem running an entire game running the same play on offense and letting opponent score on defense for purpose of determining over 5 games the expectation of one play then repeating for a handful of plays. Now if we could get maybe 3 different people on each team in the NFL putting in work over a period of a few dozen weeks, we could all develop an amazing database. We then could just look at a distribution for each play. If it is 4th and 4 what play has the greatest probability of gaining 4 yards or more? or 4th and 5? There is randomness but sometimes it is very unlikely that the randomness will play a role for some plays.
Probably it will be difficult to get enough people putting in good work cataloging everything honestly. But plays could easily be tested to verify the information is reasonably accurate.
But say you put in the work and everyone else does. Then if you can get an offense that on each given play you expect to get 10 yards or more 80% of the time you are getting 7 points starting from the 20 over 98.7% of the time. Or about 6.9 points per drive (minus whatever INT, fumbles, and etc take away directly from the expectation as well as what they add to opponent based upon strength of your D and their offense and so on.).
So if I use Christian Ponder who has a 90 short accuracy rating and only throw short routes, what completion percentage (minus drops) should I expect on those short routes?
you need to do this with every position. this is the best madden article ive ever seen.
thats a lot of math lol
For the Jets, I noticed when using Tebow, he was just as Accurate, for my purposes, as Sanchez, well done guys, also proves the GMen with Eli, are a major problem in Madden.
new member here ~ had to register after reading this article!
could you do one of these write-ups for catching? catching as you know is like throwing accuracy which has two other branches: catch in traffic and spectacular catch